Mrówka Langtona – Pokażmy Jej Nowy Kierunek
 Jarosław Piszczała
Jarosław Piszczała- 07 May, 2020
- 07 May, 2020
W poprzednim wpisie zajęliśmy się budową prostego algorytmu do prezentacji tego, jak porusza się Mrówka Langtona. Iteracyjnie rozszerzaliśmy możliwości naszego kodu od obsługi małej planszy i kilku kroków do wyświetlania dużo większej planszy z pomocą tkinter. Dziś zajmiemy się rozszerzeniem tego kodu o więcej możliwości sterowania naszą mrówką, i podziwiania jej na żywo!
Baza
Bazą do dzisiejszej pracy, będzie kod z poprzedniego wpisu. W razie potrzeb wyjaśnień warto udać się do tamtego artykułu.
import tkinter
coord_moves = { "R": {(0, -1): (-1, 0), (-1, 0): (0, 1), (0, 1): (1, 0), (1, 0): (0, -1)}, "L": {(0, -1): (1, 0), (1, 0): (0, 1), (0, 1): (-1, 0), (-1, 0): (0, -1)}, }
def create_board(size): return [[0 for _ in range(size)] for _ in range(size)]
size = 100 board = create_board(size) x, y = size // 2, size // 2 coordinates = (0, -1)
for _ in range(11000): field = board[y][x] direction = "L" if field else "R" board[y][x] = 0 if field else 1
coordinates = coord_moves[direction][coordinates] y, x = y + coordinates[0], x + coordinates[1]
root = tkinter.Tk() window_size = 400 canvas = tkinter.Canvas(root, width=window_size, height=window_size) canvas.pack()
s = window_size / size for y, row in enumerate(board): for x, field in enumerate(row): color = "white" if field == 0 else "black" canvas.create_rectangle( s * x, s * y, s + (s * x), s + (s * y), fill=color, outline=color ) root.mainloop()Algorytm w formie stringu
Na ten moment nasz algorytm opisany był poprzez if else ze względu na to, że każde pole posiadało tylko dwa stany, i od nich zależał obrót naszej mrówki. Aby móc łatwiej zmieniać algorytm, najlepiej będzie go opisać poprzez string. O dziwo, zmiana na takie podejście uprości nasz kod! Teraz, aby otrzymać kierunek poruszania, wystarczy odczytać wartość spod pozycji w naszej zmiennej pattern. Następnie zmiana wartości to dodanie jeden i użycie modulo, aby nasza wartość nie przekroczyła zakresu.
pattern = "RL"
for _ in range(11000): field = board[y][x] direction = pattern[field] board[y][x] = (field + 1) % len(pattern)
coordinates = coord_moves[direction][coordinates] y, x = y + coordinates[0], x + coordinates[1]
Po uruchomieniu mrówka zachowała się tak jak poprzednio - czyli świetnie i bez zmian!
Odcienie
Dla algorytmu z dwoma stanami kwestia kolorów jest prosta - mamy biały albo czarny. Jeżeli chcemy rozszerzyć naszą aplikację o dłuższe algorytmy, musimy zrobić coś, co odróżni te stany. Moglibyśmy użyć kolorów, ale uważam, że fajniej będzie to zrobić poprzez odcienie szarości. Będziemy je definiować na podstawie liczby możliwych stanów. W pierwszej kolejności wprowadźmy sobie pojęcie koloru w formie kodu hex. Dla koloru białego jest to #FFFFFF, dla czarnego #000000.
s = window_size / size for y, row in enumerate(board): for x, field in enumerate(row): color = "#FFF" if field == 0 else "#000" canvas.create_rectangle( s * x, s * y, s + (s * x), s + (s * y), fill=color, outline=color ) root.mainloop()Następnie dobrze byłoby utworzyć logikę do generowania odcieni. Kolory mamy tutaj w zakresach 0-255, więc musimy podzielić odpowiednio 255, aby otrzymać wartość różnicy między kolejnymi barwami. Następnie poprzez list comprehension generujemy ich listę.
color_step = int(255 / (len(pattern) - 1)) colors = [color_step * i for i in range(len(pattern))]RGB hex
To, co otrzymaliśmy na górze, to lista wartości z zakresu 0-255. Aby poprawnie użyć ich w kodzie, musimy przekształcić je na format hex. Dla przykładu RGB(255, 255, 255) jest równoznaczne z zapisem #FFFFFF. Co musimy osiągnąć, to przekształcić ją na liczbę heksadecymalną, a następnie zduplikować 3 razy, aby otrzymać ostateczny wynik. Wykorzystałem do tego formatowanie w stringach. Formatowanie zmiennej n poprzez zapis n:02x przekształci naszą liczbę na heksadecymalną (dzięki znakowi x) oraz doda 0 z przodu, jeżeli liczba w formacie heksadecymalnym będzie jednoznakowa. Pozostało powtórzyć ten manewr trzy razy i poprzedzić go znakiem #. Ostatecznie, gdy podstawimy naszą funkcję w list comprehension, otrzymamy listę gotowych kolorów do użycia!
def rgb_int_to_hex(number): return "#{n:02x}{n:02x}{n:02x}".format(n=number)
color_step = int(255 / (len(pattern) - 1)) colors = [rgb_int_to_hex(color_step * i) for i in range(len(pattern))][::-1]Pozostało użyć naszej listy barw przy kolorowaniu kwadratów podczas renderowania widoku.
Test mrówki!
Czas sprawdzić, czy kroki poczynione przez nas do tej pory pozwolą zobaczyć oczekiwane efekty. Aby przetestować więcej niż dwa kolory, postanowiłem pokazać, jak zachowa się mrówka przy algorytmie poruszania RLR. Jak widać poniżej, nasz kod wciąż działa poprawnie, obsługuje już inne, rozszerzone algorytmy i odpowiednio je prezentuje poprzez różnicę kolorów między stanami.

Stopniowe Rysowanie
Do tego momentu nasza aplikacja wyświetlała ostateczny wynik działania algorytmu. A co gdybyśmy wymusili na niej rysowanie kolejnych etapów?
Aby tego dokonać, przenieśmy kod służący do wyświetlania stanu planszy do funkcji. Na końcu tej funkcji wyląduje użycie metody canvas.update() do aktualizowania naszej kanwy.
def redraw(window_size, size, canvas, colors, board): s = window_size / size for y, row in enumerate(board): for x, field in enumerate(row): color = colors[field] canvas.create_rectangle( s * x, s * y, s + (s * x), s + (s * y), fill=color, outline=color ) canvas.update()Następnie podstawiamy ją tam, gdzie uprzednio używaliśmy tego skrawka kodu.
redraw(window_size, size, canvas, colors, board) root.mainloop()Pozostała jeszcze krokowa aktualizacja stanu. Zrobimy to w naszej pętli, która robi zmiany na naszej planszy. Na początek, aby przyspieszyć druk, będziemy odświeżać kanwę co 1000 kroków.
for i in range(15_000): field = board[y][x] direction = pattern[field] board[y][x] = (field + 1) % len(pattern)
coordinates = coord_moves[direction][coordinates] y, x = y + coordinates[0], x + coordinates[1]
if not (i % 1000): redraw(window_size, size, canvas, colors, board)Po uruchomieniu naszej aplikacji zacznie ona renderować kolejne etapy przemieszczania się mrówki, co tysiąc kroków.

Przyspieszenie Rysowania
Działa to dość wolno. Spowodowane jest to rysowaniem kolejnych kwadratów na już istniejących kwadratach. Zapychamy przez to pamięć i kanwę, która staje się coraz cięższa. Są różne metody jak poradzić sobie z tym problemem. Ja zrobię to dość prosto, poprzez dwie zmiany.
Po pierwsze, aktualnie nasza plansza nie ma podstawowej barwy, która nas interesuje. Dlatego też, przy tworzeniu obiektu klasy Canvas zdefiniujemy kolor tła.
canvas = tkinter.Canvas(root, width=window_size, height=window_size, bg="#fff")Następnie przed każdym rysowaniem nowego stanu planszy będziemy pozbywać się już istniejących elementów, i utworzymy je na nowo!
def redraw(window_size, size, canvas, colors, board): s = window_size / size canvas.delete("all") for y, row in enumerate(board): for x, field in enumerate(row): color = colors[field] canvas.create_rectangle( s * x, s * y, s + (s * x), s + (s * y), fill=color, outline=color ) canvas.update()Poniższa animacja udowadnia, że nasz skrypt zdecydowanie przyspieszył! Ale da się zrobić to jeszcze szybciej!

Kolejne przyspieszenie
Wciąż robimy pewną operację, która na ten moment jest nam niepotrzebna. Jest nią rysowanie kwadratów o kolorze białym! Skoro nasza canva ma już ustawiony podstawowy kolor, wystarczy omijać rysowanie tych kwadratów.
def redraw(window_size, size, canvas, colors, board): s = window_size / size canvas.delete("all") for y, row in enumerate(board): for x, field in enumerate(row): color = colors[field] if field: canvas.create_rectangle( s * x, s * y, s + (s * x), s + (s * y), fill=color, outline=color ) canvas.update()Aby ukazać, jak szybko teraz renderuje się mrówka, postanowiłem nie zmieniać żadnych zmiennych dotąd używanych. Różnica jest kolosalna między iteracjami naszego rozwiązania!

Pełny Zakres
Ostatni element, który jest nam potrzebny po tych zmianach, to pozwolenie mrówce działać, dopóki nie zderzy się ze ścianą. Uczynimy to poprzez zamknięcie naszego kodu w try except, dzięki czemu nasz skrypt będzie pracować wyznaczoną ilość kroków, albo do momentu zetknięcia się ze ścianą.
try: for i in range(150_000): field = board[y][x] direction = pattern[field] board[y][x] = (field + 1) % len(pattern)
coordinates = coord_moves[direction][coordinates] y, x = y + coordinates[0], x + coordinates[1]
if not (i % 1000): redraw(window_size, size, canvas, colors, board) except IndexError: print(i)Dzięki tej zmianie możemy zaobserwować jaką drogą podąża mrówka Langtona przy podstawowym algorytmie RL.

Dodatkowo dzięki tej zmianie, udało się zaobserwować błąd w naszym kodzie, który jest związany z logiką Pythona. O ile nie można wykraczać poza zakresy list, o tyle Python bez problemu obsłuży indeksy poniżej zera, z tego powodu nasza mrówka przeszła na drugą stronę! Brzmi jak fajny feature, ale by nie zakłócać wyników pozwolimy sobie go usunąć.

Ściana
Jak już wyżej opisałem, powyższy problem związany jest z możliwością poruszania się po wartościach ujemnych. Gdybyśmy chcieli, aby nasz kod wspierał takie sytuacje, należałoby wartości x oraz y przepuścić odpowiednio przez modulo. W naszym przypadku zabezpieczymy się przed tym przypadkiem, poprzez podnoszenie wyjątku IndexError, gdy któraś z wartości x lub y będzie poniżej 0.
try: for i in range(150000): field = board[y][x] direction = pattern[field] board[y][x] = (field + 1) % len(pattern)
coordinates = coord_moves[direction][coordinates] y, x = y + coordinates[0], x + coordinates[1]
if y < 0 or x < 0: raise IndexError
if not (i % 1000): redraw(window_size, size, canvas, colors, board) except IndexError: print(i)Przeniesienie zmiennych
Na koniec wyciągnijmy przydatne zmienne w jedno miejsce, aby móc łatwiej korzystać z naszego kodu!
import tkinter
coord_moves = { "R": {(0, -1): (-1, 0), (-1, 0): (0, 1), (0, 1): (1, 0), (1, 0): (0, -1)}, "L": {(0, -1): (1, 0), (1, 0): (0, 1), (0, 1): (-1, 0), (-1, 0): (0, -1)}, }
def create_board(size): return [[0 for _ in range(size)] for _ in range(size)]
def rgb_int_to_hex(number): return "#{n:02x}{n:02x}{n:02x}".format(n=number)
size = 200 pattern = "RLR" window_size = 600
steps_number = 15000 steps_render = 1000
board = create_board(size) x, y = size // 2, size // 2 coordinates = (0, -1)
color_step = int(255 / (len(pattern) - 1)) colors = [rgb_int_to_hex(color_step * i) for i in range(len(pattern))][::-1]
root = tkinter.Tk() canvas = tkinter.Canvas(root, width=window_size, height=window_size, bg="#fff") canvas.pack()
def redraw(window_size, size, canvas, colors, board): s = window_size / size canvas.delete("all") for y, row in enumerate(board): for x, field in enumerate(row): color = colors[field] if field: canvas.create_rectangle( s * x, s * y, s + (s * x), s + (s * y), fill=color, outline=color ) canvas.update()
try: for i in range(steps_number): field = board[y][x] direction = pattern[field] board[y][x] = (field + 1) % len(pattern)
coordinates = coord_moves[direction][coordinates] y, x = y + coordinates[0], x + coordinates[1]
if y < 0 or x < 0: raise IndexError
if not (i % steps_render): redraw(window_size, size, canvas, colors, board) except IndexError: print(i)
redraw(window_size, size, canvas, colors, board) root.mainloop()Zabawa Mrówką Langtona!
Zobaczmy jakie efekty możemy osiągnąć z aktualnym kodem! Dla rozmiaru planszy 300x300, oraz algorytmu RRLLLRLLLRRR prześledźmy maksymalnie 150_000 kroków, aktualizując nasz widok co 10_000 kroków.
size = 300 pattern = "RRLLLRLLLRRR" window_size = 600
steps_number = 150_000 steps_render = 10000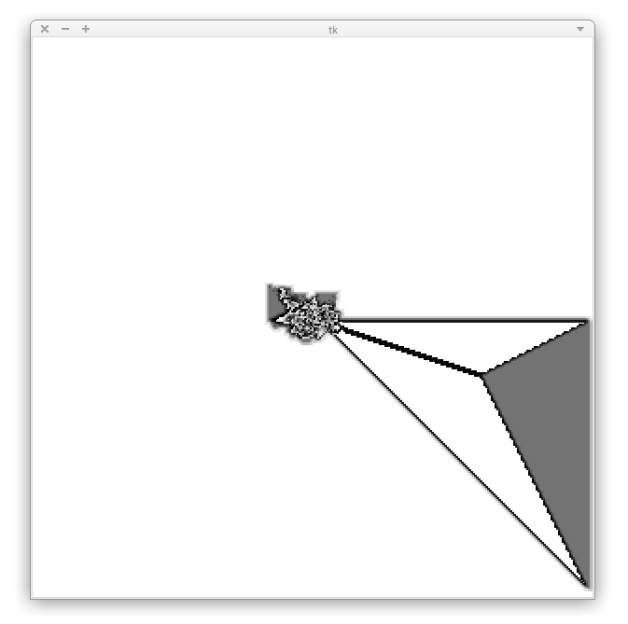
Stopka
Czy da się wycisnąć więcej z mrówki langtona? Zdecydowanie tak! Według propozycji Wikipedii mamy jeszcze dwa ciekawe przypadki do obsłużenia. Możemy dodać kolejne mrówki, oraz poruszać się po hexie! Dodatkowo wciąż wprowadzamy zmiany w kodzie, czas najwyższy przenieść sterowanie do okna aplikacji.